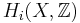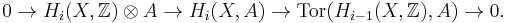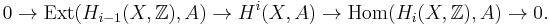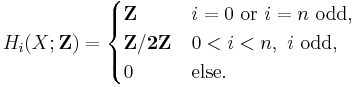Universal coefficient theorem

In mathematics, the universal coefficient theorem in algebraic topology establishes the relationship in homology theory between the integral homology of a topological space X, and its homology with coefficients in any abelian group A. It states that the integral homology groups

H_i(X, \mathbb{Z})

completely determine the groups

H_i(X, A)

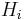Here H_i might be the simplicial homology or more general singular homology theory: the result itself is a pure piece of homological algebra about chain complexes of free abelian groups. The form of the result is that other coefficients A may be used, at the cost of using a Tor functor.

For example it is common to take A to be 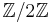\mathbb{Z}/2\mathbb{Z}, so that coefficients are modulo 2. This becomes straightforward in the absence of 2-torsion in the homology. Quite generally, the result indicates the relationship that holds between the Betti numbers bi of X and the Betti numbers bi,F with coefficients in a field F. These can differ, but only when the characteristic of F is a prime number p for which there is some p-torsion in the homology.

Contents

Statement

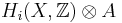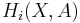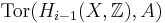Consider the tensor product H_i(X, \mathbb{Z}) \otimes A. The theorem states that there is an injective group homomorphism ι from this group to H_i(X, A), which has cokernel \mbox{Tor}(H_{i-1}(X, \mathbb{Z}), A).

In other words, there is a natural short exact sequence

0 \rightarrow H_i(X, \mathbb{Z})\otimes A\rightarrow H_i(X,A)\rightarrow\mbox{Tor}(H_{i-1}(X, \mathbb{Z}),A)\rightarrow 0.

Furthermore, this is a split sequence (but the splitting is not natural).

The Tor group on the right can be thought of as the obstruction to ι being an isomorphism.

Universal coefficient theorem for cohomology

There is also a universal coefficient theorem for cohomology involving the Ext functor, stating that there is a natural short exact sequence

0 \rightarrow \mbox{Ext}(H_{i-1}(X, \mathbb{Z}),A)\rightarrow H^i(X,A)\rightarrow\mbox{Hom}(H_i(X, \mathbb{Z}),A)\rightarrow 0.

As in the homological case, the sequence splits, though not naturally.

Example: mod 2 cohomology of the real projective space

Let 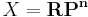X = \mathbf {RP^n}, the real projective space. We compute the singular cohomology of X with coefficients in

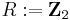R�:= \mathbf Z_2 .

knowing that the integer homology is given by:

H_i(X; \mathbf{Z}) = \begin{cases} \mathbf{Z} & i = 0 \mbox{ or } i = n \mbox{ odd,}\\ \mathbf{Z/2Z} & 0<i<n,\ i\ \mbox{odd,}\\ 0 & \mbox{else.} \end{cases}

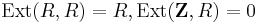We have \mathrm{Ext}(R, R)= R, \mathrm{Ext}(\mathbf Z, R)= 0 , so that the above exact sequences yield

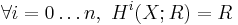\forall i = 0 \ldots n , \ H^i (X; R) = R.

In fact the total cohomology ring structure is

H^*(X; R) = R [w]/<w^{n%2B1}> .

References